Training a LSTM char-rnn in Julia to Generate Random Sentences
Generating Random Sentence with LSTM RNN
This tutorial shows how to train a LSTM (Long short-term memory) RNN
(recurrent neural network) to perform character-level sequence training
and prediction using the Julia binding of MXNet. The original model, usually called char-rnn is
described in Andrej Karpathy’s
blog, with a
reference implementation in Torch available
here.
Because MXNet.jl does not have a specialized model for recurrent neural
networks yet, the example shown here is an implementation of LSTM by
using the default FeedForward model via explicitly unfolding over time.
We will be using fixed-length input sequence for training. The code is
adapted from the char-rnn example for MXNet’s Python
binding,
which demonstrates how to use low-level
symbolic APIs
to build customized neural network models directly.
The most important code snippets of this example is shown and explained here. To see and run the complete code, please refer to the examples/char-lstm directory. You will need to install Iterators.jl and StatsBase.jl to run this example.
LSTM Cells
Christopher Olah has a great blog post about
LSTM with
beautiful and clear illustrations. So we will not repeat the definition
and explanation of what an LSTM cell is here. Basically, an LSTM cell
takes input x, as well as previous states (including c and h), and
produce the next states. We define a helper type to bundle the two state
variables together:
immutable LSTMState
c :: mx.SymbolicNode
h :: mx.SymbolicNode
end
Because LSTM weights are shared at every time when we do explicit unfolding, so we also define a helper type to hold all the weights (and bias) for an LSTM cell for convenience.
immutable LSTMParam
i2h_W :: mx.SymbolicNode
h2h_W :: mx.SymbolicNode
i2h_b :: mx.SymbolicNode
h2h_b :: mx.SymbolicNode
end
Note all the variables are of type SymbolicNode. We will construct the
LSTM network as a symbolic computation graph, which is then instantiated
with NDArray for actual computation.
function lstm_cell(data::mx.SymbolicNode, prev_state::LSTMState, param::LSTMParam;
num_hidden::Int=512, dropout::Real=0, name::Symbol=gensym())
if dropout > 0
data = mx.Dropout(data, p=dropout)
end
i2h = mx.FullyConnected(data=data, weight=param.i2h_W, bias=param.i2h_b,
num_hidden=4num_hidden, name=symbol(name, "_i2h"))
h2h = mx.FullyConnected(data=prev_state.h, weight=param.h2h_W, bias=param.h2h_b,
num_hidden=4num_hidden, name=symbol(name, "_h2h"))
gates = mx.SliceChannel(i2h + h2h, num_outputs=4, name=symbol(name, "_gates"))
in_gate = mx.Activation(gates[1], act_type=:sigmoid)
in_trans = mx.Activation(gates[2], act_type=:tanh)
forget_gate = mx.Activation(gates[3], act_type=:sigmoid)
out_gate = mx.Activation(gates[4], act_type=:sigmoid)
next_c = (forget_gate .* prev_state.c) + (in_gate .* in_trans)
next_h = out_gate .* mx.Activation(next_c, act_type=:tanh)
return LSTMState(next_c, next_h)
end
The following figure is stolen (permission requested) from Christopher Olah’s blog, which illustrate exactly what the code snippet above is doing.
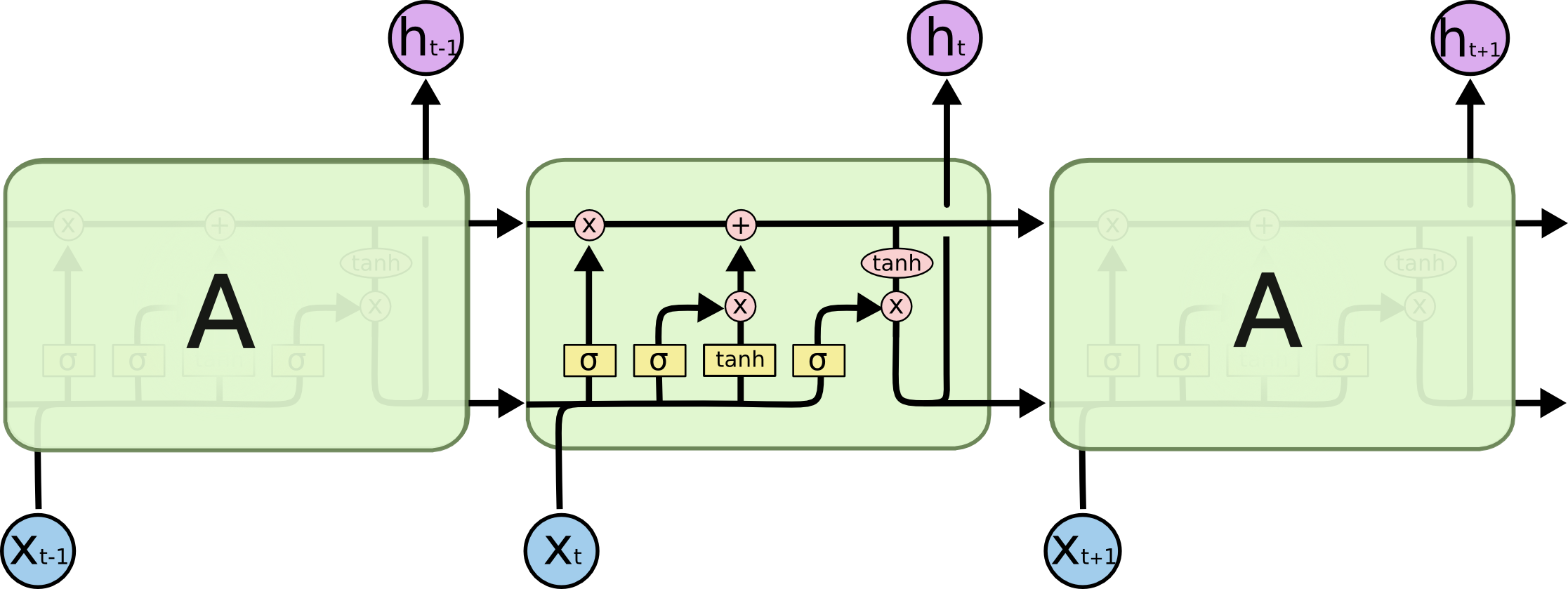
In particular, instead of defining the four gates independently, we do
the computation together and then use SliceChannel to split them into
four outputs. The computation of gates are all done with the symbolic
API. The return value is a LSTM state containing the output of a LSTM
cell.
Unfolding LSTM
Using the LSTM cell defined above, we are now ready to define a function to unfold a LSTM network with L layers and T time steps. The first part of the function is just defining all the symbolic variables for the shared weights and states.
The embed_W is the weights used for character embedding — i.e.
mapping the one-hot encoded characters into real vectors. The pred_W
and pred_b are weights and bias for the final prediction at each time
step.
Then we define the weights for each LSTM cell. Note there is one cell for each layer, and it will be replicated (unrolled) over time. The states are, however, not shared over time. Instead, here we define the initial states here at the beginning of a sequence, and we will update them with the output states at each time step as we explicitly unroll the LSTM.
function LSTM(n_layer::Int, seq_len::Int, dim_hidden::Int, dim_embed::Int, n_class::Int;
dropout::Real=0, name::Symbol=gensym(), output_states::Bool=false)
# placeholder nodes for all parameters
embed_W = mx.Variable(symbol(name, "_embed_weight"))
pred_W = mx.Variable(symbol(name, "_pred_weight"))
pred_b = mx.Variable(symbol(name, "_pred_bias"))
layer_param_states = map(1:n_layer) do i
param = LSTMParam(mx.Variable(symbol(name, "_l$(i)_i2h_weight")),
mx.Variable(symbol(name, "_l$(i)_h2h_weight")),
mx.Variable(symbol(name, "_l$(i)_i2h_bias")),
mx.Variable(symbol(name, "_l$(i)_h2h_bias")))
state = LSTMState(mx.Variable(symbol(name, "_l$(i)_init_c")),
mx.Variable(symbol(name, "_l$(i)_init_h")))
(param, state)
end
#...
Unrolling over time is a straightforward procedure of stacking the
embedding layer, and then LSTM cells, on top of which the prediction
layer. During unrolling, we update the states and collect all the
outputs. Note each time step takes data and label as inputs. If the LSTM
is named as :ptb, the data and label at step t will be named
:ptb_data_$t and :ptb_label_$t. Late on when we prepare the data, we
will define the data provider to match those names.
# now unroll over time
outputs = mx.SymbolicNode[]
for t = 1:seq_len
data = mx.Variable(symbol(name, "_data_$t"))
label = mx.Variable(symbol(name, "_label_$t"))
hidden = mx.FullyConnected(data=data, weight=embed_W, num_hidden=dim_embed,
no_bias=true, name=symbol(name, "_embed_$t"))
# stack LSTM cells
for i = 1:n_layer
l_param, l_state = layer_param_states[i]
dp = i == 1 ? 0 : dropout # don't do dropout for data
next_state = lstm_cell(hidden, l_state, l_param, num_hidden=dim_hidden, dropout=dp,
name=symbol(name, "_lstm_$t"))
hidden = next_state.h
layer_param_states[i] = (l_param, next_state)
end
# prediction / decoder
if dropout > 0
hidden = mx.Dropout(hidden, p=dropout)
end
pred = mx.FullyConnected(data=hidden, weight=pred_W, bias=pred_b, num_hidden=n_class,
name=symbol(name, "_pred_$t"))
smax = mx.SoftmaxOutput(pred, label, name=symbol(name, "_softmax_$t"))
push!(outputs, smax)
end
#...
Note at each time step, the prediction is connected to a SoftmaxOutput
operator, which could back propagate when corresponding labels are
provided. The states are then connected to the next time step, which
allows back propagate through time. However, at the end of the sequence,
the final states are not connected to anything. This dangling outputs is
problematic, so we explicitly connect each of them to a BlockGrad
operator, which simply back propagates 0-gradient and closes the
computation graph.
In the end, we just group all the prediction outputs at each time step
as a single SymbolicNode and return. Optionally we will also group the
final states, this is used when we use the trained LSTM to sample
sentences.
# append block-gradient nodes to the final states
for i = 1:n_layer
l_param, l_state = layer_param_states[i]
final_state = LSTMState(mx.BlockGrad(l_state.c, name=symbol(name, "_l$(i)_last_c")),
mx.BlockGrad(l_state.h, name=symbol(name, "_l$(i)_last_h")))
layer_param_states[i] = (l_param, final_state)
end
# now group all outputs together
if output_states
outputs = outputs ∪ [x[2].c for x in layer_param_states] ∪
[x[2].h for x in layer_param_states]
end
return mx.Group(outputs...)
end
Data Provider for Text Sequences
Now we need to construct a data provider that takes a text file, divide the text into mini-batches of fixed-length character-sequences, and provide them as one-hot encoded vectors.
Note the is no fancy feature extraction at all. Each character is simply encoded as a one-hot vector: a 0-1 vector of the size given by the vocabulary. Here we just construct the vocabulary by collecting all the unique characters in the training text – there are not too many of them (including punctuations and whitespace) for English text. Each input character is then encoded as a vector of 0s on all coordinates, and 1 on the coordinate corresponding to that character. The character-to-coordinate mapping is giving by the vocabulary.
The text sequence data provider implement the
data provider API.
We define the CharSeqProvider as below:
type CharSeqProvider <: mx.AbstractDataProvider
text :: AbstractString
batch_size :: Int
seq_len :: Int
vocab :: Dict{Char,Int}
prefix :: Symbol
n_layer :: Int
dim_hidden :: Int
end
The provided data and labels follow the naming convention of inputs used
when unrolling the LSTM. Note in the code below, apart from
$name_data_$t and $name_label_$t, we also provides the initial c
and h states for each layer. This is because we are using the
high-level FeedForward API, which has no idea about time and states. So
we will feed the initial states for each sequence from the data
provider. Since the initial states is always zero, we just need to
always provide constant zero blobs.
function mx.provide_data(p :: CharSeqProvider)
[(symbol(p.prefix, "_data_$t"), (length(p.vocab), p.batch_size)) for t = 1:p.seq_len] ∪
[(symbol(p.prefix, "_l$(l)_init_c"), (p.dim_hidden, p.batch_size)) for l=1:p.n_layer] ∪
[(symbol(p.prefix, "_l$(l)_init_h"), (p.dim_hidden, p.batch_size)) for l=1:p.n_layer]
end
function mx.provide_label(p :: CharSeqProvider)
[(symbol(p.prefix, "_label_$t"), (p.batch_size,)) for t = 1:p.seq_len]
end
Next we implement the AbstractDataProvider.eachbatch interface for the
provider. We start by defining the data and label arrays, and the
DataBatch object we will provide in each iteration.
function mx.eachbatch(p :: CharSeqProvider)
data_all = [mx.zeros(shape) for (name, shape) in mx.provide_data(p)]
label_all = [mx.zeros(shape) for (name, shape) in mx.provide_label(p)]
data_jl = [copy(x) for x in data_all]
label_jl= [copy(x) for x in label_all]
batch = mx.DataBatch(data_all, label_all, p.batch_size)
#...
The actual data providing iteration is implemented as a Julia
coroutine. In this way, we can write the data loading logic as a
simple coherent for loop, and do not need to implement the interface
functions like Base.start, Base.next, etc.
Basically, we partition the text into batches, each batch containing several contiguous text sequences. Note at each time step, the LSTM is trained to predict the next character, so the label is the same as the data, but shifted ahead by one index.
#...
function _text_iter()
text = p.text
n_batch = floor(Int, length(text) / p.batch_size / p.seq_len)
text = text[1:n_batch*p.batch_size*p.seq_len] # discard tailing
idx_all = 1:length(text)
for idx_batch in partition(idx_all, p.batch_size*p.seq_len)
for i = 1:p.seq_len
data_jl[i][:] = 0
label_jl[i][:] = 0
end
for (i, idx_seq) in enumerate(partition(idx_batch, p.seq_len))
for (j, idx) in enumerate(idx_seq)
c_this = text[idx]
c_next = idx == length(text) ? UNKNOWN_CHAR : text[idx+1]
data_jl[j][char_idx(vocab,c_this),i] = 1
label_jl[j][i] = char_idx(vocab,c_next)-1
end
end
for i = 1:p.seq_len
copy!(data_all[i], data_jl[i])
copy!(label_all[i], label_jl[i])
end
produce(batch)
end
end
return Task(_text_iter)
end
Training the LSTM
Now we have implemented all the supporting infrastructures for our char-lstm. To train the model, we just follow the standard high-level API. Firstly, we construct a LSTM symbolic architecture:
# define LSTM
lstm = LSTM(LSTM_N_LAYER, SEQ_LENGTH, DIM_HIDDEN, DIM_EMBED,
n_class, dropout=DROPOUT, name=NAME)
Note all the parameters are defined in
examples/char-lstm/config.jl.
Now we load the text file and define the data provider. The data
input.txt we used in this example is a tiny Shakespeare
dataset.
But you can try with other text files.
# load data
text_all = readall(INPUT_FILE)
len_train = round(Int, length(text_all)*DATA_TR_RATIO)
text_tr = text_all[1:len_train]
text_val = text_all[len_train+1:end]
data_tr = CharSeqProvider(text_tr, BATCH_SIZE, SEQ_LENGTH, vocab, NAME,
LSTM_N_LAYER, DIM_HIDDEN)
data_val = CharSeqProvider(text_val, BATCH_SIZE, SEQ_LENGTH, vocab, NAME,
LSTM_N_LAYER, DIM_HIDDEN)
The last step is to construct a model, an optimizer and fit the mode to
the data. We are using the ADAM optimizer in this example.
model = mx.FeedForward(lstm, context=context)
optimizer = mx.ADAM(lr=BASE_LR, weight_decay=WEIGHT_DECAY, grad_clip=CLIP_GRADIENT)
mx.fit(model, optimizer, data_tr, eval_data=data_val, n_epoch=N_EPOCH,
initializer=mx.UniformInitializer(0.1),
callbacks=[mx.speedometer(), mx.do_checkpoint(CKPOINT_PREFIX)], eval_metric=NLL())
Note we are also using a customized NLL evaluation metric, which
calculate the negative log-likelihood during training. Here is an output
sample at the end of the training process.
...
INFO: Speed: 357.72 samples/sec
INFO: == Epoch 020 ==========
INFO: ## Training summary
INFO: NLL = 1.4672
INFO: perplexity = 4.3373
INFO: time = 87.2631 seconds
INFO: ## Validation summary
INFO: NLL = 1.6374
INFO: perplexity = 5.1418
INFO: Saved checkpoint to 'char-lstm/checkpoints/ptb-0020.params'
INFO: Speed: 368.74 samples/sec
INFO: Speed: 361.04 samples/sec
INFO: Speed: 360.02 samples/sec
INFO: Speed: 362.34 samples/sec
INFO: Speed: 360.80 samples/sec
INFO: Speed: 362.77 samples/sec
INFO: Speed: 357.18 samples/sec
INFO: Speed: 355.30 samples/sec
INFO: Speed: 362.33 samples/sec
INFO: Speed: 359.23 samples/sec
INFO: Speed: 358.09 samples/sec
INFO: Speed: 356.89 samples/sec
INFO: Speed: 371.91 samples/sec
INFO: Speed: 372.24 samples/sec
INFO: Speed: 356.59 samples/sec
INFO: Speed: 356.64 samples/sec
INFO: Speed: 360.24 samples/sec
INFO: Speed: 360.32 samples/sec
INFO: Speed: 362.38 samples/sec
INFO: == Epoch 021 ==========
INFO: ## Training summary
INFO: NLL = 1.4655
INFO: perplexity = 4.3297
INFO: time = 86.9243 seconds
INFO: ## Validation summary
INFO: NLL = 1.6366
INFO: perplexity = 5.1378
INFO: Saved checkpoint to 'examples/char-lstm/checkpoints/ptb-0021.params'
Sampling Random Sentences
After training the LSTM, we can now sample random sentences from the trained model. The sampler works in the following way:
- Starting from some fixed character, take
afor example, and feed it as input to the LSTM. - The LSTM will produce an output distribution over the vocabulary and a state in the first time step. We sample a character from the output distribution, fix it as the second character.
- In the next time step, we feed the previously sampled character as input and continue running the LSTM by also taking the previous states (instead of the 0 initial states).
- Continue running until we sampled enough characters.
Note we are running with mini-batches, so several sentences could be sampled simultaneously. Here are some sampled outputs from a network I trained for around half an hour on the Shakespeare dataset. Note all the line-breaks, punctuations and upper-lower case letters are produced by the sampler itself. I did not do any post-processing.
## Sample 1
all have sir,
Away will fill'd in His time, I'll keep her, do not madam, if they here? Some more ha?
## Sample 2
am.
CLAUDIO:
Hone here, let her, the remedge, and I know not slept a likely, thou some soully free?
## Sample 3
arrel which noble thing
The exchnachsureding worns: I ne'er drunken Biancas, fairer, than the lawfu?
## Sample 4
augh assalu, you'ld tell me corn;
Farew. First, for me of a loved. Has thereat I knock you presents?
## Sample 5
ame the first answer.
MARIZARINIO:
Door of Angelo as her lord, shrield liken Here fellow the fool ?
## Sample 6
ad well.
CLAUDIO:
Soon him a fellows here; for her fine edge in a bogms' lord's wife.
LUCENTIO:
I?
## Sample 7
adrezilian measure.
LUCENTIO:
So, help'd you hath nes have a than dream's corn, beautio, I perchas?
## Sample 8
as eatter me;
The girlly: and no other conciolation!
BISTRUMIO:
I have be rest girl. O, that I a h?
## Sample 9
and is intend you sort:
What held her all 'clama's for maffice. Some servant.' what I say me the cu?
## Sample 10
an thoughts will said in our pleasue,
Not scanin on him that you live; believaries she.
ISABELLLLL?
See Andrej Karpathy’s blog post on more examples and links including Linux source codes, Algebraic Geometry Theorems, and even cooking recipes. The code for sampling can be found in examples/char-lstm/sampler.jl.
Visualizing the LSTM
Finally, you could visualize the LSTM by calling to_graphviz on the
constructed LSTM symbolic architecture. We only show an example of
1-layer and 2-time-step LSTM below. The automatic layout produced by
GraphViz is definitely much less clear than Christopher Olah’s
illustrations,
but could otherwise be very useful for debugging. As we can see, the
LSTM unfolded over time is just a (very) deep neural network. The
complete code for producing this visualization can be found in
examples/char-lstm/visualize.jl.
